【徹底解説】パスキーの仕組み！次期マイナカードでも採用予定のECDSAとは？

近年、パスワードに依存しない新しい認証方式として「パスキー」が注目されています。パスキーはしばしば「パスワードを使わず、指紋や顔認証でログインできる最新技術」と説明されますが、この説明だけでは“生体認証だから安全”という誤解を生みがちです。逆に、「指紋や顔のデータが外部サーバーに送られてしまうのでは」という不安を抱く人もいます。

しかし、パスキーの仕組みを理解すると、指紋や顔認証はあくまで“スマホ内部の鍵を開くための手段”にすぎず、安全性を支えている本質はパスキーそのものの暗号技術ECDSAにあります。また、生体情報がサーバーに送信されることはありません。

さらに、量子コンピュータの登場によって暗号解析能力が向上し、パスキーを含むセキュリティ技術への不安も語られています。では、パスキーで使われている暗号技術ECDSAとは何なのでしょうか。

これらの疑問を解消するために、AIに質問して学んだ内容を共有します。私は専門家ではありませんので、解釈に誤りがある可能性もありますが、その点はあらかじめご了承ください。

こちら↓の記事の続きになります。

パスキーとは
ECDSAの仕組み
楕円曲線暗号の基本知識
ECDSAの弱点
量子コンピュータで何が危険か？
1. 狙われる数式：楕円曲線上の「掛け算」の逆
  1. 今のコンピュータ（古典コンピュータ）の世界
2. Q と d の対応表を作れるのでは？
  1. 量子コンピュータの世界
パスキーで ECDSA が使われることの「凄さ」
まとめ

パスキーとは

パスキーは、スマートフォンの指紋認証や顔認証、セキュリティキーを使って安全にログインできる仕組みです。ここでいう「キー」とは、実際にはスマホ内部で生成される“秘密鍵”と、サーバーに登録される“公開鍵”という2つの暗号鍵のことを指します。

指紋認証や顔認証は、この秘密鍵を取り出すための“鍵の金庫を開ける手段”にすぎません。ログイン時には、スマホが秘密鍵を使ってサーバーからのチャレンジに署名し、サーバーは公開鍵でその署名を検証することで本人確認を行います。

この仕組みの中核を担っているのが楕円曲線暗号による電子署名アルゴリズムECDSA であり、特に「P-256（secp256r1）」と呼ばれる楕円曲線が最も広く利用されています。

これから、実際のユースケースで、どのようにECDSAが動いているのかを見ていきます。

ECDSAの仕組み

ECDSA（Elliptic Curve Digital Signature Algorithm：楕円曲線デジタル署名アルゴリズム）は、「誰が書いたか（本人確認）」と「書き換えられていないか（改ざん検知）」を証明するための技術です。

パスキーの他、ビットコインやイーサリアムなどのブロックチェーン、ウェブサイトのHTTPS通信（TLS）などで広く使われています。

パスキーにおいて、ECDSAがどう動いているのか、「登録（鍵を作るとき）」と「認証（ログインするとき）」の2つの場面に分けて解説します。

登録フェーズ（鍵ペアの生成）

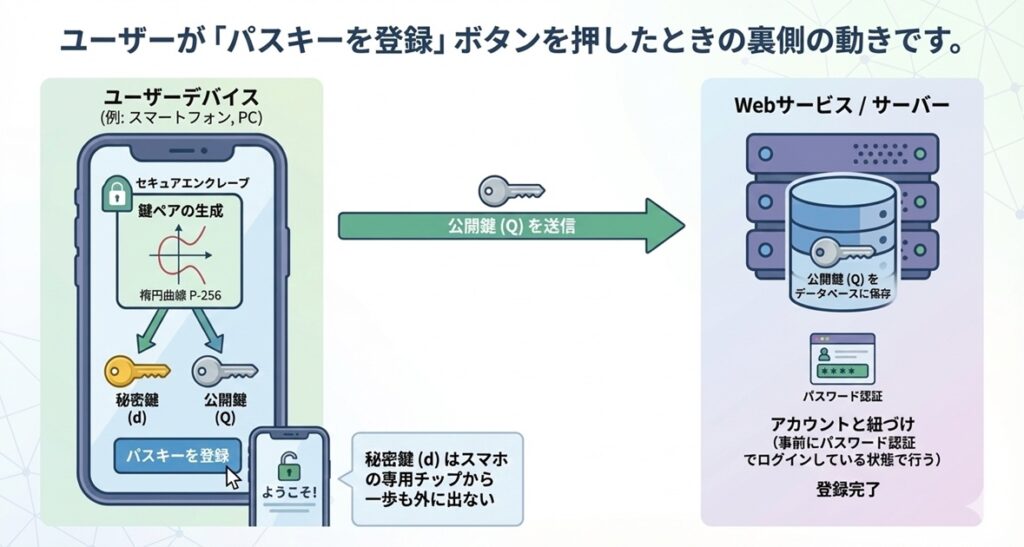
ユーザーが「パスキーを登録」ボタンを押したときの裏側の動きです。

鍵ペアの生成:
- あなたのスマホの中で、楕円曲線（ P-256など）を使って秘密鍵 (d ) と 公開鍵 ( Q ) のペアを作ります。
  秘密鍵 (d): スマフォの秘密の数字（例: d=12345 ）
  公開鍵 (Q): Q=d×G（秘密鍵d回だけGを足した点のx,y座標、楕円曲線上の点の足し算の仕方は後述）
- 基準点Gは、楕円曲線上の点で、ECDSA P–256やP-384という定数セット（後述）の中で定義されているx,y平面上の座標です。
- 秘密鍵 (d ) はスマホの専用チップ（セキュアエンクレーブやTitan Mなど）から一歩も外に出ません。
公開鍵の送信:
- 公開鍵 ( Q ) だけをサーバー（GoogleやAppleなど）に送ります。
- サーバーは、これをデータベースに「このユーザーの公開鍵」として保存します。
- ここの作業は、アカウントと紐づけなければならないので、事前にパスワード認証でサーバーにログインしている状態で行うことになります。

これでパスキーを使う準備が整いました。次に、ログインするときの動きを見ていきます。

認証フェーズ（ECDSAによるログイン）

ここが ECDSA の出番です。ユーザーが「ログイン」ボタンを押したときの動きです。

簡潔に言うと、サーバーが送るチャレンジ（ランダムな値）とドメイン情報に対して、スマホが秘密鍵で“署名”し、サーバーは公開鍵でその署名を検証することで、スマホが本物の秘密鍵を持っていることを確認する仕組みです。
「簡易的な楕円曲線で足し算を解説」を先に読んだ方が、イメージしやすいと思います。

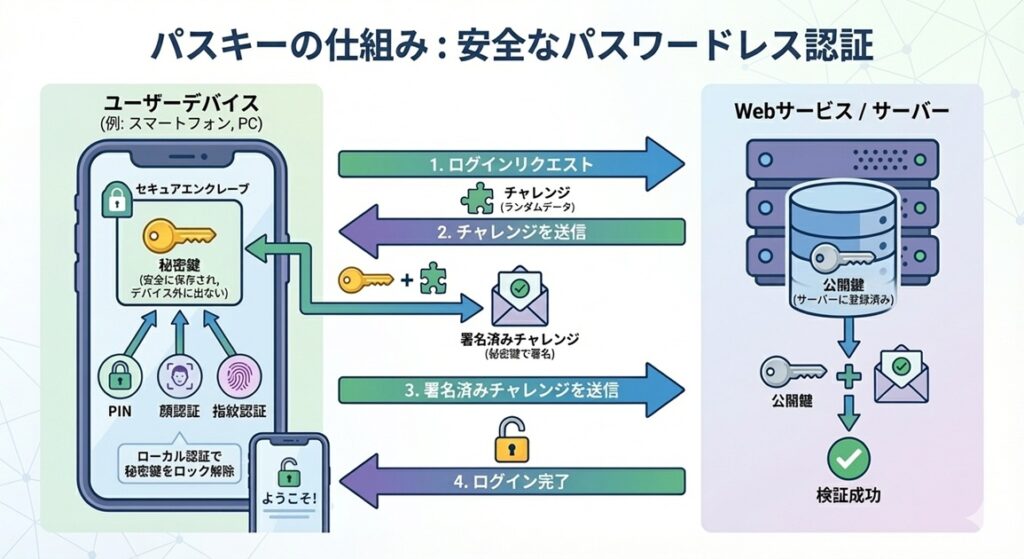
Step 1: サーバーからの挑戦状 (Challenge)

サーバーは、ログインしようとしているユーザーに対し、ランダムなデータ（チャレンジ）を送ります。

「このランダムな数字『8f7a2…』に、君の秘密鍵で署名をして送り返してくれ」
これは、後ほどの解説における「署名対象データ: チャレンジ」に相当します。

Step 2: 本人確認 (User Verification)

スマホ画面に認証画面が出て生体認証（指紋・顔認証）やPINなどの入力を求めてきます。

顔認証や指紋認証が成功すると、スマホ内部の専用チップにある秘密鍵 ( d ) へのアクセスが許可されます。
※ 生体情報はサーバーには送られません。あくまで「秘密鍵の金庫を開ける鍵」として使われます。

Step 3: 署名の作成 (Signing)

スマホは以下のデータをまとめて、ECDSA署名を行います。

署名対象データ: チャレンジ + ドメイン情報（例: google.com）

手順:

ハッシュ値z: 署名対象データをハッシュ関数に通して、数値 zに変換します。（ハッシュとは長い文章を固定長の数字にする処理です。同じ入力なら必ず同じ結果になり、少しでも変えると全く違う値になる“デジタル指紋”のようなものです。）
乱数 k の生成: ここが超重要です。 署名のたびに、一時的な秘密の乱数 k （ナンス）を作ります。
点Rの計算: 乱数kを使って、楕円曲線上の点Rを計算します。
- R=k×G
- この点 Rの x座標 を取り出し、これをrと呼びます。
署名sの計算: 以下の式でsを計算します。
s=(z+r×d)/k mod n
- z: 署名対象データのハッシュ
- r: 点Rのx座標
- d: スマフォの秘密鍵
- k: さっきの乱数
- n: 基準点 G の位数（オーダー）（ECDSA P–256やP-384という定数セットの中で定義されている定数、後述）

ここで「mod n（割り算のあまり）」というのは、数字がぐるっと一周する特別な計算ルール（有限体）のことです。時計が 12 を超えると 1 に戻るのと同じで、使える数字の範囲を 0〜n−1 に限定するだけの仕組みです。そのためs=(z+r×d)/k mod nで計算されるsは0～n-1の範囲に収まります。

この mod n は「値を範囲内に収めるための調整」にすぎないため、概念を説明する際には省略しても式の本質は変わりません。以降の説明ではsの式からmod nは省略します。

結果: この(r,s)のペアが「デジタル署名」です。スマフォはメッセージ（署名対象データ）と一緒にこの(r,s)をサーバーに送ります。

Step 4: サーバーによる検証 (Verification)

サーバー（検証する人）は、スマフォから「署名対象データ（メッセージ）」「署名(r,s)」を受け取ります「スマフォの公開鍵Q」はサーバーに事前に登録されています。サーバーはスマフォの秘密鍵dも、乱数kも知りませんが、計算だけで「正しいか」確認できます。

手順:

ハッシュ化:署名対象データ（メッセージ）をハッシュ化してzを出します。（スマフォと同じことをやっているので、同じ値になります。）
逆数の計算: 署名sの逆数 w=1/sを計算します。
確認用の点 Pを計算: 以下の式で、楕円曲線上の点Pを作ります。
P=(z×w)×G+(r×w)×Q
- 基準点G：ECDSA P–256やP-384という定数セット（後述）の中で定義されている定数
- スマフォの公開鍵Q
- 署名r
判定: 計算して出てきた点Pの x座標 が、署名のrと一致すれば合格です。ログイン成功となります。

まとめ

作成: 乱数 kで点Rを作り、秘密鍵dを混ぜて署名 (r,s)を作る。
検証: 署名(r,s)と公開鍵Qを使って点Rを復元（再現）し、一致するか確かめる。一致するということは秘密鍵dをスマフォが持っていることの証。（後述）
幾何学: 楕円曲線の「点乗算」の一方向性（計算は簡単、逆算は無理）のおかげで安全性が保たれています。←この文章は後述する楕円曲線上の点の足し算方法を見ると足すのは簡単だけど、結果（最終点）から、1個前の点を見つけるのは難しいことがイメージつきます。「逆算が無理」な件は後述します。

なぜこれで証明できるのか？（幾何学的な意味）

検証の式

P=(z×w)G+(r×w)Q

ステップ 1: 検証の式に「公開鍵」を代入する

検証者が行う計算のスタート地点は以下の式です。

𝑃=(𝑧×𝑤)𝐺+(𝑟×𝑤)𝑄

ここに、公開鍵の定義𝑄=𝑑×𝐺を代入します。

𝑃=(𝑧×𝑤)𝐺+(𝑟×𝑤)(𝑑×𝐺)

ステップ 2:𝐺でまとめる（因数分解）

楕円曲線の計算では、スカラー（普通の数字）の掛け算は順序を入れ替えても結果は変わりません。また、同じ点𝐺が掛かっている場合は、普通の計算のように「くくりだす」ことができます。

第2項の(𝑟×𝑤)(𝑑×𝐺)を整理すると、(𝑟×𝑤×𝑑)𝐺になります。
式全体を𝐺でまとめます。

𝑃=(𝑧×𝑤+𝑟×𝑤×𝑑)×𝐺

さらに、共通している𝑤も括弧の外にくくりだします。

𝑃=𝑤×(𝑧+𝑟×𝑑)×𝐺

だいぶシンプルになりました。ここで「括弧の中身 (𝑧+𝑟×𝑑) 」に注目してください。

ステップ 3: 署名の式を変形して𝑘を見つける

ここで一旦、署名作成時の式を思い出して、式変形をします。

署名の式：𝑠=(𝑧+𝑟×𝑑)/𝑘
補足：mod nは省略。
この式の両辺に𝑘を掛け、両辺を𝑠で割る（つまり𝑘と𝑠を入れ替える）と、以下の形になります。

𝑘=(𝑧+𝑟×𝑑)/𝑠

ここで、𝑤=1/𝑠だったので、1/𝑠を𝑤に置き換えると…

𝑘=𝑤×(𝑧+𝑟×𝑑)

驚くべきことに、ステップ2で整理した式の「𝐺の係数部分」と、この「𝑘の式」が完全に一致しました！

𝑃=𝑘×𝐺

つまり署名の作成に使った式を逆算しているだけです。

k×Gといえば……そう、スマフォが最初に作った点Rのことです。
つまり検証とは、「スマフォが秘密裏に作った点Rの場所を、サーバーがもっている情報 ( s,r,Q,G,z) だけを使ってサーバーが再現できるか？」 というパズルを解いているのです。
注意：rを求めるのが検証の目的ではありません。rの値自体は送ってるので、値はいくつか分かっています。検証の式で出したPがRになるかを検証してます。
これが一致するということは、数式の中に「本物の秘密鍵d」が含まれていなければ絶対にあり得ないため、スマフォ本人が署名したと証明されます。

楕円曲線暗号の基本知識

ECDSAで使われる楕円曲線をどんなものか？
楕円曲線の加算の方法を見ていきます。
まず、DCDSAで主に使われている楕円曲線のｐ-256の場合、以下になります。

P-256の主な仕様

パラメータ	値 / 特徴
方程式	y^2=x^3 – 3x + b (mod p)
係数 a	-3 に固定されています（計算効率を上げるため）。
素数 p（後述）	2^256 – 2^224 + 2^192 + 2^96 – 1 (計算機で処理しやすい特殊な形の素数が選ばれています)
係数 b	非常に大きな乱数のような値（NSAが生成したシード値から導出されています）。
ベースポイント G	曲線上の基準となる生成元（始点）。

簡易的な楕円曲線で足し算を解説

楕円曲線上の点の加算方法がイメージできるとECDSAの全体像が見えてきます。

注意点（誤解しやすいところ）：
・楕円曲線暗号で使われる計算はx,y平面上の楕円曲線のある点（Gなどと表記）を加算してるだけ。ただし、加算は(x1+x2,y1+y2)というように各x,y座標をそれぞれ加算するのではなく専用の加算方法がある。
・kGとはG + G + G + …（k 回、Gを加算）ということ。注意：（kx,ky）ではない。

簡単な楕円曲線y^2 = x^3 – 3x + 5を例に加算を可視化しました。左側で途切れているように見えるのは、描画範囲の都合で切れているのではなく、そのx座標より左には数式の解となる実数が存在しないためです。つまり、そこが曲線の本来の端点です。

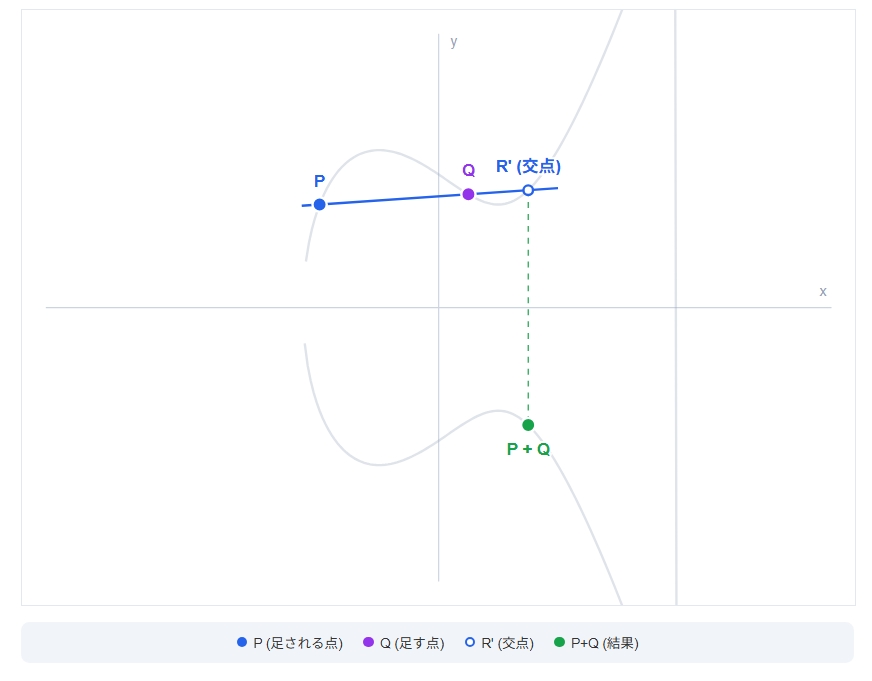
異なる点の加算 (Addition)

操作: 2つの点 P と Q を結ぶ「直線（コード）」を引く。
幾何学: 直線は曲線のどこかでもう1点（ R′）と交わる。
結果: その交点 R′ を X軸で折り返した点 が P+Q になる。

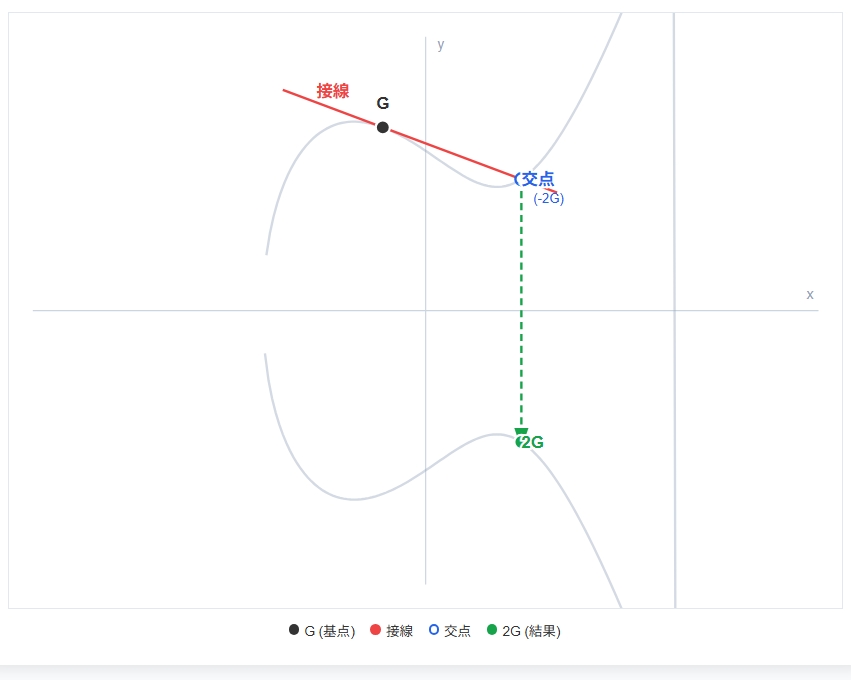
同じ点の加算 (Doubling)

操作: 点 G における「接線（タンジェント）」を引く。
幾何学: 接線は曲線のどこかでもう1点G′（図では-2Gと書いてあります。）と交わる。
結果: その交点 G′ を X軸で折り返した点 がG+G、（２G）になる。

奇数の場合 ( 3G ) の計算手順

今回は最もシンプルな例として、3G( =2G+G )を求めます。
「kが2の乗数（2, 4, 8, 16…）のとき」は、ひたすら接線を引く「2倍算（Doubling）」だけで済みます。しかし、「kが奇数（や2の乗数以外）のとき」は、「異なる2点の足し算（Addition）」を組み合わせる必要があります。

3Gを一発で求める線はありません。以下の2ステップに分解します。

Step 1: 2Gを作る（同じ点の加算＝接線）

Gに接線を引いて、折り返して 2Gを作ります。

Step 2: 2G+Gをする（異なる点の加算＝直線）

ここで「2G（さっき作った点）」と「G（最初の点）」を足します。

操作: 点 G と点 2G を通る直線を引きます。
交点: その直線が曲線と交わる場所を探します。
折り返し: 交点をX軸で折り返した場所が、3Gです。

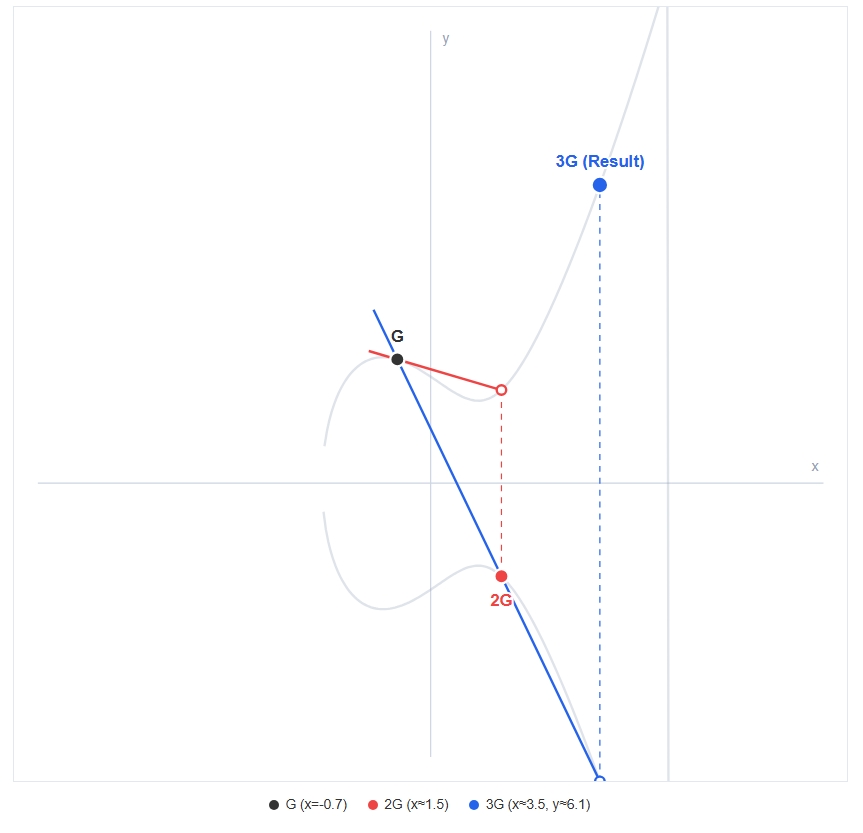
このように、「2倍算」で作った点に、さらに「元の点」を足し合わせることで、あらゆるkG（kが奇数含む）の計算が可能になります。

なぜ「折り返し」が必要なのか？

補足として、なぜ最後に必ず「X軸で折り返す」のか、その理由を直感的に説明します。

楕円曲線のルールでは、「一直線上にある3つの点を足すとゼロ（無限遠点）になる」 と定義されています。
P+Q+R′=0
これを移項すると、以下のようになります。
P+Q=−R′
楕円曲線のグラフはX軸対称なので、ある点R′のマイナス（逆元）である−R′は、X軸の反対側の点（座標でいうと(x,−y) ）になります。

だから、「交点R′を求めて、それをひっくり返す」という操作が、計算の最後には必ず必要になるのです。

例外がひとつだけあります

もし、2点を結んだ線が「垂直（Y軸と平行）」になった場合はどうなるでしょうか？（例：Pと、その真下にある−Pを足した場合）

垂直な線は、どこまで伸ばしても曲線の「3つ目の点」と交わりません。
この場合、答えは「定義不能」ではなく、「無限遠点 (O )」 という架空のゼロ地点に飛ぶことになっています。
式で書くと P+(−P)=0 です。

P-256 や P-384 とは「定数セット」の名前

「P-256」というのは単なる曲線の名前ではなく、以下の6つの数字のセット（ドメインパラメータ）を指す規格名です。

p : 素数（座標 x,y を計算するための時計の大きさ）
a : 曲線の係数 a（ y^2 = x^3 + ax + b の係数）
b : 曲線の係数 b （ y^2 = x^3 + ax + b の係数）
G : 基準点（ベースポイント）の座標 (x,y)
n : 基準点 G の位数（オーダー）
h : 余因子（通常は1）

これらは NIST（米国国立標準技術研究所）などの標準化団体によって、「セキュリティ上安全で、計算効率が良い数値」として固定されています。

定数 n の具体的な中身

n は「基準点 G を何回足したら無限遠点（ゼロ）になるか」という回数を表す巨大な素数です。無限遠点は楕円曲線の足し算における“ゼロ（単位元）”として定義されているため、 n 回足すと無限遠点になり、さらに G を足すと元の位置 G に戻ります。

つまり、この n が秘密鍵 d の取りうる範囲（1〜n−1）を決めています。

P-256 の n は 256 ビットの素数なので、秘密鍵 d も約 256 ビットの整数になります。

また、公開鍵 Q は Q = d × G で計算されるため、取りうる公開鍵の種類も秘密鍵と同じく n−1 個です。

nは、それぞれの規格で値が決まっています。

P-256 (secp256r1) の場合

パスキーで最も使われる規格です。

n (10進数):
115792089210356248762697446949407573529996955224135760342422259061068512044369
特徴: 約256ビットの大きさです。

P-384 (secp384r1) の場合（2026年の次期マイナンバーカードで採用される）

より高いセキュリティが必要な場合（政府機関など）に使われます。

n (10進数):
39402006196394479212279040100143613805079739270465446667948293404245721771496870329047266088258938001861606973112319
特徴: 約384ビットの大きさです。桁数が全然違うことがわかります。

mod pとmod nについて

modを使う目的は、数字が大きくならないように抑え込む目的があります。

p (Prime Field): 座標用
- x 座標や y 座標を計算するときに使います。
- y^2=x^3+ax+b(mod p)
- グラフ用紙の「広さ」を決める数字です。
n (Order): 署名・秘密鍵用
- 秘密鍵dや署名s、乱数kを計算するときに使います。
- s=k−1(z+rd)(mod n)
- 「使える秘密鍵のパターンの数」を決める数字です。

なぜ使い分ける？
ハッセの定理（Hasse’s theorem）という数学の定理により、nの値はpの値と「だいたい同じ大きさ」にはなりますが、正確には違う数値（違う素数）になります。
そのため、

座標の計算（点の足し算）をしているときは mod p
署名の計算（スカラ倍の計算）をしているときは mod n

というように、厳密に使い分けられています。

modとは?

🌱 mod（モッド）とは？

mod n とは「n で割った余り（あまり）」のことです。

たとえば：

14 mod 5 → 14 を 5 で割った余り → 4
27 mod 7 → 27 を 7 で割った余り → 6
10 mod 10 → 余り → 0

⏰ 時計の例で説明すると分かりやすい

「時計は 12 で一周する mod 12 の世界」

たとえば：

10 時に 5 時間後 → 10 + 5 = 15
でも時計では 3 時
→ 15 mod 12 = 3
23 時 → 23 mod 12 = 11（つまり 11 時）

つまり時計は、

数字が 12 を超えたら 0 〜 11 に戻る仕組み

これが mod と同じ考え方です。

🍰 ケーキの例（シンプルな余り）

ケーキが 10 切れあるとします。

あなたが 23 人に配るとき、
10 切れ × 2 回（20 切れ）配れますが、3 切れ余ります。

つまり：

[
23 \mod 10 = 3
]

🎯 mod を使うと何がうれしいの？

✔ 数がどれだけ大きくなっても

0 〜 n−1 の範囲におさまる

たとえば、n = 10 の世界だと：

1000 mod 10 → 0
9999 mod 10 → 9
123456 mod 10 → 6

どれだけ大きな数でも
「最後の一桁だけ」になるのと同じような感覚です。

💡 mod n の世界は「数字がループする世界」

普通の数字はずっと大きくなっていきますが、
mod n の世界では…

**n まで行くと 0 に戻る

→ ぐるぐる回る世界（ループ）**

図にするとこんな感じ：

0 → 1 → 2 → … → n−1 → 0 → 1 → …

🔐 ECDSA で mod n が使われる理由（やさしく）

ECDSA や暗号では、数字がものすごく大きくなります。

でも、

使っていい数字の範囲
→ 0〜n−1 だけ（これが決まり）

だから計算の途中で数字が大きくなっても、

mod n で「あまり」に変えて範囲に戻す必要がある。

これが
[
s = k^{-1}(z + rd) \mod n
]
の意味です。

🧁 最終まとめ（初心者向け）

mod n = n で割った余り
数が大きくなっても 0〜n−1 に戻るルール
時計と同じで ぐるぐる回る世界
暗号では使える数字の範囲が決まっているので
mod でその範囲に戻す

ECDSAの弱点

「乱数k」は絶対に使い回してはいけません。

もしスマフォが、違うメッセージに対して同じ乱数kを使って署名してしまうと、数学的な引き算をするだけで、スマフォの秘密鍵dが逆算されてバレてしまいます。

「乱数 k（ナンス）」が重複すると、楕円曲線暗号の堅牢な守りが、単なる中学校レベルの連立方程式にまでレベルダウンしてしまい、秘密鍵 d が誰でも計算できるようになってしまいます。

なぜ「引き算するだけ」でバレてしまうのか、その数学的なカラクリをわかりやすく解説します。

ECDSA署名の計算式（基本）

まず、署名 s がどのように作られるかを確認します。簡略化した式は以下の通りです。

s=(z+r×d)/k mod n

s: 署名の一部
k: その都度生成すべき乱数
z: メッセージのハッシュ値
r: 乱数 k から作られる座標（k が同じなら r も同じになる）
d: 絶対に守りたい秘密鍵
n: 定数（曲線の位数）

この式を変形すると、以下の形になります。

ks=z+r×d mod n

通常、ここには「未知数」が k と d の2つあるため、この方程式を解くことはできません（変数が2つで式が1つ）。

乱数 k を使い回すと何が起きるか

ここで、スマホが2つの違うメッセージ（ハッシュ値 z1 と z2）に対して、誤って同じ乱数 k を使って署名してしまったとします。

すると、攻撃者は、通信ログやブロックチェーンから以下の2つの式を手に入れます。（s1、s2、z1、z2は具体的にいくつか分かってしまった状態。）

署名1: ks1 = z1 + rd
署名2: ks2 = z2 + rd

ここが重要です：

k が同じなので、r（kから生成される値）も同じになります。つまり、上の2つの式にある rd（秘密鍵を含む項）が全く同じ値になってしまいます。

秘密鍵がバレる手順（引き算）

攻撃者は、この2つの式を「引き算」します。

(k-s1) – (k-s2)= (z1 + rd) – (z2 + rd)

k (s1 – s2) = z1 – z2

ご覧の通り、邪魔だった秘密鍵の項 (rd) が消えました。

残ったのは k だけです。あとは割り算（モジュラ逆数）をするだけで k が求まります。

k = (z1 – z2)/(s1 – s2)

(※厳密にはモジュラ逆数 (s_1 – s_2)^-1 を掛けます)

最後に秘密鍵 d を逆算

一度 k がバレてしまえば、ゲームオーバーです。

最初の署名の式 s1 = k^-1(z1 + rd) に、判明した k を代入して式変形すれば、秘密鍵 d が求まります。

d = (s1k – z1)/r

これで、攻撃者はあなたのスマホの秘密鍵を完全に入手しました。

歴史的な大事故の実例

この「k の使い回し」は理論上の話ではなく、実際に巨大な事故を引き起こしています。

PlayStation 3 (2010年):ソニーはECDSAの実装で、あろうことか乱数 $k$ を固定値にしてしまいました。ハッカーチーム（fail0verflow）はこれに気づき、上記の手順で署名鍵（ルートキー）を特定。結果、PS3上で自作ソフトが自由に動かせるようになりました。
Androidの脆弱性 (2013年):Androidの乱数生成器（SecureRandom）にバグがあり、一部のビットコインウォレットアプリで k が衝突する事象が発生。実際に多くのビットコインが盗まれました。

解決策：RFC 6979

現在、まともな暗号ライブラリでは、この事故を防ぐためにRFC 6979という規格（Deterministic ECDSA）を採用しています。

仕組み: 乱数k を「サイコロ」で決めるのではなく、「秘密鍵」と「メッセージ」を混ぜてハッシュ化した値を使います。
メリット:
- 同じメッセージには必ず同じk が生成される。
- 違うメッセージには必ず違うk が生成される。
- 乱数生成器の品質が悪くても、k が衝突する事故が物理的に起きない。

「もしスマフォが、違うメッセージに対して同じ乱数 k を使って署名してしまうと、数学的な引き算をするだけで、秘密鍵 d が逆算されてバレてしまいます。」

これはECDSAの最も恐ろしい性質であり、「乱数生成器（RNG）の品質が、システム全体の命運を握っている」と言われる理由です。

量子コンピュータで何が危険か？

結論から申し上げますと、量子コンピュータによって計算（突破）されてしまう可能性があるのは、公開鍵 Q から秘密鍵 d を逆算する部分です。

現在のコンピュータでは「宇宙の寿命より長い時間がかかる」とされているこの計算が、量子コンピュータにとっては「現実的な時間で解ける計算」になってしまいます。

具体的に、どの数式のどの部分が狙われるのかを解説します。

狙われる数式：楕円曲線上の「掛け算」の逆

ECDSAの安全性の根幹は、以下の数式の性質に依存しています。

Q = d × G

d: 秘密鍵（あなたが持っている、非常に大きな整数）
G: ベースポイント（みんなが知っている、曲線の始点）
Q: 公開鍵（公開する座標。パスキーで使われる ECDSA では相手サーバーのみに送られるが、HTTPS の TLS では誰でも取得できる形で公開されている。）

今のコンピュータ（古典コンピュータ）の世界

d × G → Q (順方向):秘密鍵 d から公開鍵 Q を作るのは一瞬です（数ミリ秒）。これを「スカラー倍算」と呼びます。
Q / G → d (逆方向):公開鍵 Q と始点 G から、秘密鍵 d を割り出す（逆算する）のは不可能です。これを「楕円曲線離散対数問題 (ECDLP)」と呼びます。

Q と d の対応表を作れるのでは？

Q = d × GのGは定数で、みんな知っている値なので
Q(q1x,q1y)=G→d=1
Q(q2x,q2y)=2G→d=2
Q(q3x,q4t)=3G→d=3
というようにQの座標とdの一覧ができてしまうのではないでしょうか。

結論から言うと：

理論上は「Q = dG の一覧表」を作れます。しかし、現実的には絶対に作れません。
理由は、一覧表が“宇宙の物質を全部集めても足りないほど巨大”になるからです。

ここを直感的に、かつ数学的に正確に説明します。

🔥 結論：一覧表は「作れるはず」だが、実際には絶対に作れない

G は公開されている
d は 1〜n−1
Q = dG
ならば d=1,2,3… と順番に計算して Q を並べれば
「d と Q の対応表」が作れるはず

これは数学的には完全に正しい発想です。

しかし、現実には絶対に不可能です。

🚀 なぜ不可能なのか？理由は「n が巨大すぎる」から

P-256 の n は約 1.15 × 10^77 という巨大な素数です。

つまり、秘密鍵 d の候補は：

約 10⁷⁷ 個

これはどれくらいかというと…

🌌 宇宙の原子の総数：10⁸⁰ 個　🔢 d の候補数：10⁷⁷ 個

→ 宇宙の原子の数と同じレベル

📚 一覧表を作るにはどうなる？

一覧表のサイズは：

1 行につき Q の座標（x,y）＝ 256ビット × 2
1 行 ≈ 64バイト
行数 ≈ 10⁷⁷ 行

必要な容量は：

64 バイト × 10^77 = 6.4 × 10^78 バイト

これは…

地球の全データ容量（約 10²¹ バイト）の 10⁵⁷ 倍
宇宙全体の物質を全部ハードディスクにしても足りない

つまり、

一覧表を作るための物質が宇宙に存在しない。

🧠 では計算で求めればいいのでは？

「一覧表を作らなくても、Q を見て d を探せばいいのでは？」

と思うかもしれません。

しかし、Q = dG の逆計算は 楕円曲線離散対数問題（ECDLP） と呼ばれ、

既知のどんなアルゴリズムでも、
2²⁵⁶ 回の試行が必要（＝宇宙の寿命を超える）

ということが数学的に分かっています。

量子コンピュータの世界

量子コンピュータが Shor のアルゴリズムを使えば ECDLP を解けると言われていますが、

実用的に P-256 を破るには 数千万〜数億量子ビットの誤り訂正済み量子コンピュータが必要
現在の量子コンピュータは 数百量子ビットレベル

つまり、現実的にはまだ破れません？

パスキーで ECDSA が使われることの「凄さ」

単にパスワードの代わりになっているだけではなく、ECDSAの仕組みを応用して強力なセキュリティを実現しています。

1. フィッシング詐欺が数学的に不可能

パスキーの署名には、「どのサイトで署名したか（Origin）」という情報が強制的に混ぜ込まれます。

もしあなたが「偽のGoogleサイト（g00gle.com）」に誘導され、そこで指紋認証をしてしまっても、作成される署名は「g00gle.com用」の署名になります。
本物のGoogleのサーバーがその署名を検証しようとしても、ハッシュ値 z が食い違うため、数式上で絶対に一致しません。
人間が騙されても、楕円曲線は騙されないのです。
しかし、そこでパスワード入力を要求してくる場合は気を付けたほうがいいです。偽サイトにパスワードを知られたら元も子もありません。

2. リプレイ攻撃の防止

サーバーが毎回違う「チャレンジ（ランダムな値）」を送ってくるため、署名結果(r,s)は毎回全く違う値になります。

攻撃者が通信を盗聴して「さっきの署名データ」をコピーして後で送っても、サーバーは「いや、今のチャレンジは違う値だから無効だ」と弾くことができます。

まとめ

パスキーの安全性を支えている本質は、指紋認証や顔認証といった“見える部分”ではなく、その裏で動く ECDSA（楕円曲線デジタル署名）という暗号技術です。生体認証はあくまで、スマートフォン内部にある秘密鍵へアクセスするための“金庫の鍵”にすぎません。

また、この ECDSA は量子コンピュータ時代における安全性の議論でも中心にあり、「公開鍵から秘密鍵を逆算されるのでは」という懸念が語られるのも、この仕組みを理解すると理由がよくわかります。

さらに、ECDSA はパスキーだけの技術ではなく、次期マイナンバーカードにも採用予定の重要な暗号方式です。つまり、私たちの生活インフラの根幹に組み込まれていく技術でもあります。

こうした背景を知っておくと、「量子耐性暗号が必要になる理由」「マイナンバーカードの更新で何が変わるのか」「パスキーがなぜフィッシングに強いのか」といった IT ニュースの意味が一気にクリアになります。

ECDSA を理解することは、これからのデジタル社会を読み解く“リテラシー”そのものです。

この記事を書いたイチゲを応援する（質問でもokです）
Vプリカでのお支払いがおすすめです。

MENTAやってます（ichige）