病院の窓口にある「顔認証付きカードリーダー」で、マイナンバーカードがどのように使われているのか。 この記事では、その裏側で動いている 暗号技術(特に RSA) に焦点を当てて、できるだけ分かりやすく解説します。
私は専門家ではありませんが、AI に質問しながら丁寧に調べました。しかし、解釈に誤りがある可能性もありますので、その点はあらかじめご了承ください。
前半でマイナンバーカードの仕組みを病院の窓口のカードリーダーとe-Taxの例をもと解説。
後半でRSAの仕組みを見る構成になっています。
注意)本記事では、べき乗を^で表記しています。
マイナンバーカードに入っている情報(ICチップの中身)
まず、カードリーダーが読み取っている「ICチップ」の中身を整理します。今回の解説に関係する部分だけを抜粋します。
券面(印刷されている情報)
- 氏名
- 住所
- 生年月日
- 性別
- 顔写真
- マイナンバー(裏面)
ICチップ内
マイナンバーカードで最も重要なのは、公開鍵と秘密鍵です。特に秘密鍵はIC チップ内から絶対に出ません。
暗証番号や顔認証で利用権限が得られても、外部に出てくるのは
- 秘密鍵で計算した結果(署名や暗号化データ)
だけです。秘密鍵そのものが漏れることはありません。
① 電子証明書
- 利用者証明用電子証明書(病院の窓口などで使用)
- 証明書の発行番号(証明書ごとで違う)(注1)
- 利用者証明用公開鍵
- 認証局(CA)の署名
- 署名用電子証明書(e-taxなどで使う)
- 証明書の発行番号(証明書ごとで違う)(注1)
- 基本4情報(氏名・住所・性別・生年月日)(注1)
- 署名用公開鍵
- 認証局の署名
② 秘密鍵(チップ外に出ない)
- 利用者証明用秘密鍵
- 署名用秘密鍵
③パスワード(そのまま保存されているわけではない)
- 署名用電子証明書のパスワード(6〜16文字英数字)
- 利用者証明用電子証明書のパスワード(4桁 数字)
- 券面事項入力補助のパスワード(4桁 数字)
- 住民基本台帳用のパスワード(4桁 数字)
- 署名用電子証明書、利用者証明用電子証明書には、それぞれ公開鍵が入っています。この公開鍵は、秘密鍵とペアになっていて、有効期限が5年です。5年の根拠は、ずっと同じだと心配だということだと思います。公開鍵は秘密鍵とペアなので、両方変わるし、公開鍵がはいっている証明書も変わるので認証機関の署名も変わります。これらの変更をICチップにする必要があるため、ネットで済ますことができず役場に行く必要が出てきます。
- 署名用電子証明書、利用者証明用電子証明書は改ざんされないように認証局の署名が入っています。これにより、署名用電子証明書、利用者証明用電子証明書にはいっているそれぞれの公開鍵の改ざんを防いでいます。
■ 公開鍵の有効期限は5年
公開鍵と秘密鍵はペアであり、公開鍵が入っている電子証明書にも有効期限があります。 期限が切れると、カードの IC チップに新しい証明書を書き込む必要があるため、役所で更新手続きが必要になります。
■ 証明書は改ざんされないよう CA の署名付き
電子証明書には、認証局(CA)が行った電子署名が付いています。 これにより、
- 公開鍵が改ざんされていない
- 本物の証明書である
ことが保証されます。
■ 利用者証明用電子証明書には「基本4情報」が入っていない
ここが非常に重要です。
利用者証明用電子証明書には 氏名・住所などの基本4情報が入っていません。
そのため、この証明書だけでは「誰のものか」を判別できません。
後述する Step 6 で、発行番号を使って J-LIS に照会し、署名用電子証明書と紐付ける ことで個人を特定します。
注1)
公的個人認証サービス利用のための 民間事業者向けガイドライン22ページから引用
利用者証明用電子証明書には、基本4情報が記録されていないため、単体ではその電子証明書が誰に紐付くものであるかを判別することができない。そこで、民間事業者が利用者証明用電子証明書を利用する場合には、利用者ごとの「利用者識別情報」と「利用者証明用電子証明書」を紐付ける必要がある。そのための方法として、同一個人宛てに発行された「署名用電子証明書の発行番号(「シリアル番号」のことをいう。以下同様。)」を基に「利用者証明用電子証明書の発行番号」を機構に照会する方法が有効と考えられる。
「署名用電子証明書」には基本4情報が記録されているため、それを基に、「利用者識別情報と署名用電子証明書を紐付ける」ことが可能である。
「基本4情報」とは氏名、住所、性別、生年月日。
これから説明する病院の窓口の例は、「利用者証明用電子証明書」のみカードから送信され、「署名用電子証明書」は送信してないことを前提としてます。
公開鍵暗号方式とデジタル署名のしくみ
必要な基礎知識です。
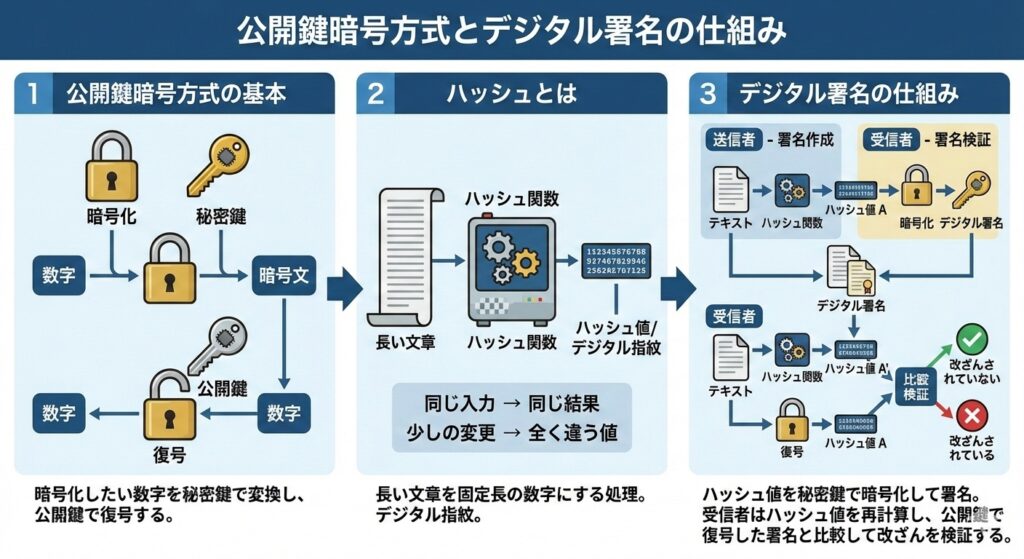
マイナンバーカードで使われている具体的な暗号方式はRSAです。後ほど詳しく解説します。
ハッシュ関数とは
ハッシュ関数は、どんな長さのデータでも固定長の「ハッシュ値(デジタル指紋)」に変換する仕組みです。
特徴:
- 元のデータに戻せない
- 1文字違うだけで全く別の値になる
マイナンバーカードでは SHA-256 が使われています。
SHA-256の具体例
入力:
abc
SHA-256 の出力(ハッシュ値):
ba7816bf8f01cfea414140de5dae2223
b00361a396177a9cb410ff61f20015ad
入力:
abd
出力(SHA-256):
88d4266fd4e6338d13b845fcf289579d
209c897823b9217da3e161936f031589
SHA-256 の出力は256ビットです。例示されている数字は、見やすいように0と1のビット列を16進数に変換して表示しています。なので、例示した出力は16進数表記で64個すが、ビット表記(01で表記)すると256個(ビット)になります。
👉 たった1文字違うだけで、完全に別物の出力になる。
これが SHA の強さ。UTF-8 とパディング
実際には、
- 文字列を UTF-8 に変換
- パディング処理で 512bit の倍数に揃える
といった前処理を行ってからハッシュ化します。
abcは実際に計算されるときはutf-8でエンコードされたものが使われます。
例
abc→61 62 63
あ→e3 81 82
また「61 62 63」をそのままハッシュ関数に入れるのではなく、パディング処理(データの後ろに決まった形式で1ビットの1と0を追加し、最後に元データのビット長を付けて、入力サイズを512ビットの倍数に揃える作業)を行ってから入力します。UTF-8については、こちら↓で解説しています。
病院の窓口で行われている処理の流れ(オンライン資格確認の技術フロー)
ここからは、病院の窓口でマイナンバーカードを使ったときに、 裏側でどんな処理が行われているのか を、技術的なステップとともに解説します。
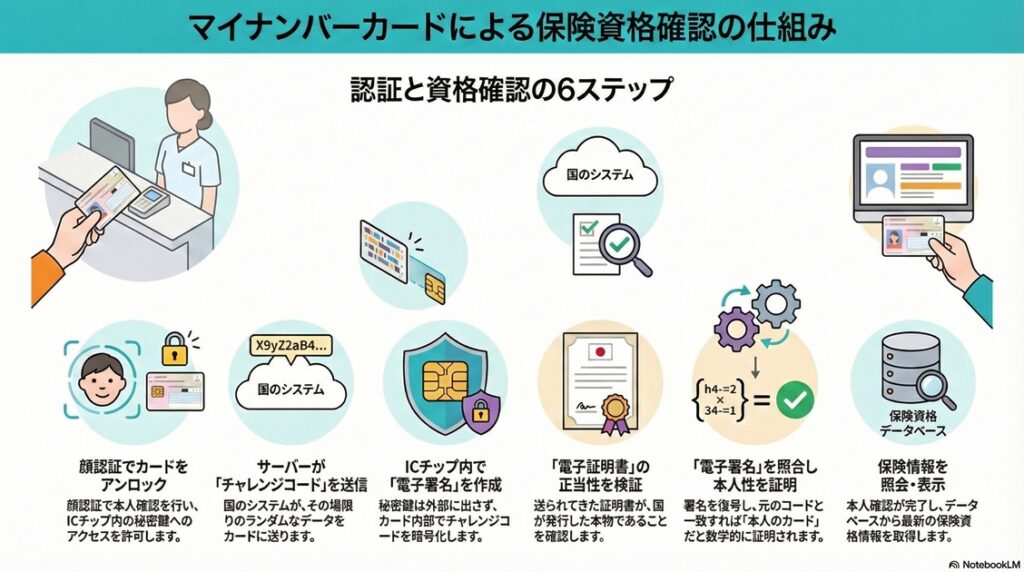
この図の補足説明
サーバーに送り返しているものは
・「チャレンジコード」(ICチップ内で電子署名したもの)
・「電子証明」=「利用者証明用電子証明書」(病院の窓口の例の場合)
図は概略なので、下の解説をお読みください。
Step 1: カードセットとアクセス権の解除
要約:本人確認(顔認証 or 4桁PIN)で、ICチップ内の秘密鍵の利用権限が解除される。
患者がカードをリーダーに置くと、IC チップ内の重要機能(電子証明書・秘密鍵)はまだロックされています。
- 顔認証の役割:
カードを置いた瞬間、リーダーはCANを読み取ります。この数字をパスワードとしてICチップに入力し、ICチップ内の「顔写真データ」にアクセスします。これをカメラで撮影した顔と照合します。一致すると「本人確認済み」となり、ICチップ内の利用者証明用秘密鍵へのアクセス権(利用権限)がアンロックされます。(顔認証を使わない場合は、利用者証明用電子証明書のパスワード4桁を使用します)
注意:顔認証部分については、Geminiの回答を使ってます。(ChatGptは、チップに顔のデータは入っておらず係員が人力で確認してると答えた。)
カードの中に顔の情報は入っているようです。参考:次期個人番号カード仕様に係る検討事項についての41ページに「ICチップでは券面事項確認AP内に顔写真データを格納している」
Step 2: サーバーからの「チャレンジ」
要約:サーバーがランダムな乱数(チャレンジコード)をカードに送る。
病院の端末は、国の「オンライン資格確認システム」へ接続します。
システム側は、その場限りのランダムなデータ(乱数)を生成し、これを チャレンジコード としてカードに送ります。
内容は:
「この乱数(チャレンジコード)を、あなたの秘密鍵で署名して返してください」
という要求です。
Step 3: ICチップ内での「電子署名」
要約:秘密鍵は外に出ず、IC チップ内でチャレンジコードに署名する。
カードリーダーは、チャレンジコード(Challenge)をICチップに送り込みます。
IC チップ内の CPU が、保存されている 利用者証明用秘密鍵 (N, d) を使って次の計算を行います。
Signature = Challenge^d mod N ← この式の意味は後述の「RSAの仕組み」をご覧ください。
計算結果である「電子署名 (Signature)」と、「利用者証明用電子証明書(発行番号+公開鍵 (N,e) +認証局の署名)」だけが、外部に送られます。
✔ 秘密鍵そのものは絶対に外に出ない
ここがマイナンバーカードの最重要ポイントです。
Step 4: 利用者証明用電子証明書の検証
要約:送られてきた証明書が本物かどうかを、CA の公開鍵で検証する。
サーバーはまず、カードから送られてきた 利用者証明用電子証明書 が本物かどうかを確認します。
① 証明書には「公開鍵+発行番号+認証局の署名」が入っている
マイナンバーカードの電子証明書には、次のような情報が入っています:
- 公開鍵(N,e)
- 発行番号
- 発行した認証局(CA)の情報
- これら全部をまとめたデータに対する CA の電子署名
つまり証明書は、
「この公開鍵と発行番号は、この人のものですよ」
「これは国(認証局)が保証しますよ」
という“署名付きの宣言文”です。
② 認証局(CA) を検証する
証明書の最後には、認証局(CA)が
署名 = Hash(証明書の内容)^dca mod Nca
という CA の秘密鍵(Nca,dca)で作った電子署名が付いています。これはマイナンバーカードを作ったときにICに書き込まれます。
病院のシステムや e-Tax のサーバーは、あらかじめ認証局の公開鍵(Nca,eca)(ルート証明書)を持っているので、次のように検証できます:
復号 = 署名^eca mod Nca
同時にサーバーは送られてきた証明書のハッシュ値を求めます。
これが復号した値と一致すれば、
- 証明書は改ざんされていない
- 本当に国の認証局が発行したもの
- 中に入っている公開鍵(N,e)と発行番号は正当なもの
と確認できます。
- 失効チェック(CRL):
さらに、紛失届などで証明書が無効化されていないか、失効リスト(CRL)で確認します。
Step 5: チャレンジコード検証
要約:公開鍵で署名を復号し、元の乱数(チャレンジコード)と一致すれば「本人のカード」と証明される。
証明書が本物だと分かったので、ようやく中の「公開鍵 (N,e)」を使います。
システムは、公開鍵 (N,e) を使って、Step 3で送られてきた「電子署名(Signature)」を検証(復号)します。
Decrypted = Signature^e mod N
この計算結果が、最初に送った「チャレンジコード(元の乱数)」と完全に一致するかを確認します。
- 【ここでの証明内容】一致した場合、
「この公開鍵は本人の秘密鍵とペアである」
「その秘密鍵を持っているのは「今、カードを使っている人」だけ」
と数学的に証明されます。
ということは利用者証明用電子証明書の中の発行番号も秘密鍵とペアであり、この発行番号は「今、カードを使っている人」のものだということが証明できます。
Step 6: 保険情報の照会と個人特定
要約:発行番号を使って J-LIS に照会し、署名用電子証明書と紐付けて個人を特定する。
ここで多くの人が疑問に思う点があります。
「利用者証明用電子証明書には基本4情報が入っていないのに、どうやって個人を特定しているの?」
● 仕組みはこうです
- サーバーは、利用者証明用電子証明書の 発行番号(シリアル番号) を J-LIS に照会
- J-LIS のデータベースでは、
- 利用者証明用電子証明書
- 署名用電子証明書(基本4情報入り) が内部で紐付けられている
- 署名用電子証明書側の 基本4情報(氏名・住所など) を参照し、個人を特定
- 特定された個人に紐づく 保険資格情報(保険者番号・負担割合など) を返す
【結果】
こうして最終的に、病院のモニターには名前と共に「資格あり(負担割合3割)」といった結果が表示されます。
e-Taxでのマイナンバーカード利用
ここでは、マイナンバーカードが e-Tax(電子申告)でどのように使われているか を解説します。
まず利用者識別番号を作る
e-Tax を利用するには、国税庁が管理する 利用者識別番号(16桁) が必要です。
重要な点:
- 利用者識別番号は マイナンバーカードには入っていない
- 税務署が管理する「あなたの納税者ID」
- マイナンバーカードの電子証明書とは別物
よく混同されるので注意が必要です。
■ e-Tax で必要な2つの情報
| 種類 | どこにある? | 役割 |
|---|---|---|
| 利用者識別番号(16桁) | 国税庁のデータベース | あなたの納税者ID |
| 署名用電子証明書のパスワード(6〜16文字) | マイナンバーカード内 | 電子署名を行うためのPIN |
この2つは桁数が似ているため、混乱しやすいポイントです。
電子署名の流れ
e-Taxでの一連の流れ
| Step | 行動 | 裏側の処理 | 使うもの |
| 1. ログイン | e-Taxソフトやコーナーにログインする | 認証(Authentication) 「このカードを持ってきたのは、利用者識別番号xxxxの人だな」とシステムが認識してログインさせる。 | 数字4桁の暗証番号 (利用者証明用電子証明書のパスワード) |
| 2. 作成 | 申告書を作る | サーバー上でデータを作成・保存。 | (特になし) |
| 3. 送信準備 | 「送信」ボタンを押す | 電子署名(Signature) 作成した申告書データ(XMLファイル)のハッシュ値を署名用秘密鍵で署名する。 | 英数字6-16文字のパスワード (署名用電子証明書のパスワード) |
| 4. 受信通知 | 送信完了 | 国税庁は、届いたデータについている「署名」を確認し、紐付いている「利用者識別番号」のフォルダに格納する。 | – |
れにより、
- データが改ざんされていない
- 確かに本人が送信した
ことが確認されます。
重要な点
- 署名処理はカード内で完結
- PCやスマホは秘密鍵に触れない。(データのハッシュ値をカードICに送って、秘密鍵で署名された値をもらうだけなので秘密鍵の値は分からない。)
つまり、マルウェアに感染していても、 秘密鍵を盗まれるリスクは極めて低くなっています。
RSA の仕組み(ざっくり)
ここからは、マイナンバーカードでも使われている RSA暗号の仕組み を、できるだけ分かりやすく説明します。
実際の RSA は 2048bit など巨大な数を使いますが、ここでは理解のために 小さな数字 を使います。
RSA では、
- 公開鍵(みんなに見せてOK(TLSなどの場合)、マイナンバーカードのように、みんなに見せないで済む用途の場合見せない。)
- 秘密鍵(本人だけ)
の2つを作ります。
数学的には
- 公開鍵 → (N, e)
- 秘密鍵 → (N, d)
という組み合わせで表現されます。
まずは「素数を2つ選ぶ」
RSAは 素数 p, q を使います。
簡単にするため、めちゃくちゃ小さい素数にします:
p = 5
q = 11N を作る
N = p × q = 5 × 11 = 55この 55 が公開鍵の一部になります。
φ(N) を計算する
φ(ファイ)はオイラーのトーシェント関数。
φ(N) = φ(p)×φ(q)=(p - 1) × (q - 1)
= 4 × 10
= 40
補足:オイラーのトーシェント関数(φ関数)とは、自然数 𝑛 に対して「1から 𝑛 までの整数のうち、𝑛 と互いに素な数の個数」を表す関数です。 つまり、最大公約数が1になる数を数える関数です
例:
𝜑(6)=2(1と5が6と互いに素)𝜑(7)=6(7は素数なので、1~6すべてが互いに素、つまり素数-1になりp-1やq-1が上式に出てきた理由です。)
また、積の性質(互いに素な素数)の場合𝜑(pq)=𝜑(p)×𝜑(q)という性質があります。
e を決める(公開鍵の指数)
条件:
- φ(N) と互いに素
- 小さい数字でOK
よく使われるのは 3, 17, 65537 などですが
ここでは e = 3 にします。
e = 3
d を求める(秘密鍵の指数)
これは
d × e ≡ 1 (mod φ(N))
を満たす d を求めます。
つまり
d × 3 を 40 で割った余りが 1
となる d を探す。
小さいので総当たりします:
| d | 3×d | 40で割った余り |
|---|---|---|
| 13 | 39 | 39 |
| 14 | 42 | 2 |
| 27 | 81 | 1 ←これ! |
✔ よって
d = 27公開鍵と秘密鍵が完成
- 公開鍵 = (N, e) = (55, 3)
- 秘密鍵 = (N, d) = (55, 27)
これで暗号と復号ができます。
実際に暗号化してみる
送りたいメッセージを数字 M にするとします。
(実際のRSAはデータを整数に変換します)
ここでは小さくして M = 7 とします。
暗号化(公開鍵を使う):
C = M^e mod N
= 7^3 mod 55
= 343 mod 55
343 を 55 で割ると…
343 ÷ 55 = 6 余り13
✔ 暗号文は
C = 13
復号してみる(秘密鍵を使う)
受け取った C=13 を復号化:
M = C^d mod N
= 13^27 mod 55
この計算が大変です。関数電卓をお持ちでない場合以下の方法がありますが、それでも大変です。
べき乗計算サイトhttps://keisan.site/exec/system/1294758675
mod計算サイトhttps://ja.wolframalpha.com/input/?i=10+mod+3(べき乗も入力できるかもしれないが入力方法が不明)
ということで下のPythonがおすすめ!
PythonのPOW関数を使うと累乗計算(べき乗)が簡単
Pythonのpow()関数は、累乗計算(べき乗)を行う組み込み関数で、3つ目の引数を指定すると剰余演算(mod計算)を高速に処理できます。暗号や数論の分野でもよく使われる重要な関数です
pow(base, exp) # baseのexp乗
pow(base, exp, mod) # (baseのexp乗)をmodで割ったあまり
例
print(pow(2, 3)) # 8 (2^3)
print(pow(2, 3, 5)) # 3 ((2^3) % 5)13^27 mod 55を求めてみます。
result1 = pow(13, 27, 55)
print(f"pow()を使用: 13^27 mod 55 = {result1}")
結果
pow()を使用: 13^27 mod 55 = 7✔ 元のメッセージ 7 が戻ってきました!
まとめ(小さな数字で理解するRSA)
| ステップ | 内容 |
|---|---|
| 1 | 2つの素数 p, q を選ぶ |
| 2 | N = p×q を計算 |
| 3 | φ(N) を計算 |
| 4 | e(公開鍵指数)を選ぶ |
| 5 | d(秘密鍵指数)を求める |
| 6 | 公開鍵 = (N, e)、秘密鍵 = (N, d) 完成 |
| 7 | 暗号化:C = M^e mod N |
| 8 | 復号化:M = C^d mod N |
RSAの安全性の根拠は? 公開鍵(e と N )が分かっても 秘密鍵d が求められない理由は?
公開鍵としてeとNは公開されています。なのになぜ秘密鍵をdを求めるのは難しいのでしょうか?
答えは、φ(N) が分からないから
そして φ(N) が分からない理由は、N を素因数分解できないからです。
d を求めるには φ(N) が必要
秘密鍵 d は次の合同式を満たす数です:
d × e ≡ 1 (mod φ(N))
これは「e の φ(N) における逆元」を求める問題です。
逆元を求めるのは簡単です。
でも φ(N) が分からないと逆元は計算できません。
逆元とは?
逆元(ぎゃくげん)とは、ある演算(足し算や掛け算など)において、与えられた要素と演算すると単位元(たんいげん)になるような別の要素のことです。
例えば、加法では数𝑎 の逆元は-𝑎(+)、乗法では𝑎 の逆元は(𝑎×(1/𝑎)=1)で、これらはそれぞれの演算の単位元(加法の単位元は、乗法の単位元は)に対応します。この概念は、暗号技術などで使われる法𝑁 での逆元(モジュラ逆数)など、より一般的に代数系で扱われます。
具体例
- 加法 (足し算):
- 単位元:0
- の逆元:(例:3 の逆元は -3)
- 乗法 (掛け算):
- 単位元:1
- 𝑎 の逆元: または 𝑎^−1 (例:3 の逆元は )
- 剰余(法 Ncap N𝑁 での計算):
- 𝑎×𝑏≡1(mod𝑁) を満たす 𝑏 が 𝑎 の逆元(𝑎^−1 (mod 𝑁))。
φ(N) を求めるには N の素因数分解が必要
RSA では
N = p × q
という 2 つの巨大な素数の積を使います。
そして
φ(N) = (p-1)(q-1)
なので、φ(N) を求めるには p と q を知る必要があります。
RSAの仕組みで使った例では
φ(N) = φ(p)×φ(q)=(p - 1) × (q - 1)
= 4 × 10
= 40
これだったらp、qは小さい数字なので、p、qを総当たりで代入していけば、
すぐp = 5、q = 11が見つかります。つまり、この例のNはp×q=55と2桁です。N の素因数分解が「現実的に不可能」だから安全
公開されているのは N と e だけ。
でも φ(N) を求めるには N を素因数分解して p と q を取り出す必要がある。
ところが、RSA で使われる 2048bit(約617桁)の N を素因数分解するのは、
- 現代のスーパーコンピュータでも
- 宇宙の寿命より長い時間がかかる
と言われています。
つまり、
N を素因数分解できない → φ(N) が分からない → d が求められない
という構造で安全性が成り立っています。
他の RSA 解説動画で使われている例を検証してみる
参考にした2つの動画の RSA 例についても、実際に計算して確認してみます。
2つともわかりやすい説明なので、ぜひご覧ください。
動画1
こちらhttps://www.youtube.com/watch?v=FmoOn5HFNx4で使っているもの実践してみます。
暗号化
公開鍵e=5、n=323=17×19(pとqは17と19)
秘密鍵d=29、n=323
平文11を公開鍵で暗号化する式→11^5 mod 323
11^5=161,051
よって161,051 mod 323→暗号文197
復号化
暗号文197を秘密鍵で平文に戻す式→197^29 mod 323
197^29=3.463542799821930199322E+66
動画で使われているこの計算ができる関数電卓があればいいが、ないのでPythonを使う。
result1=pow(197,29,323)
print(f"pow()を使用: 13^27 mod 55 = {result1}")
結果
pow()を使用: 13^27 mod 55 = 11←平文に戻ったのでOK!動画2
こちらのhttps://youtu.be/lzkygPvMRbU?si=aL2HvJMkVFEB61Dyで使っているもの実践してみます。
暗号化
公開鍵e=3、n=55=5×11(pとqは5と11)
秘密鍵d=7、n=55
平文13(動画の最初の1文字)を公開鍵3で暗号化する式→13^3 mod 55
暗号文52
result1=pow(13,3,55)
print(result1)
結果
52復号化
暗号文52を秘密鍵7で平文に戻す式→52^7 mod 55
result1=pow(52,7,55)
print(result1)
結果
13←平文に戻ったのでOK!こちらの動画では秘密鍵dの算出方法が今まで説明してきたものと違いますが、より小さい数に抑える手法かもしれません。
こちらの再生リストを最初から見ることをお勧めします。https://youtube.com/playlist?list=PL5Pahvi5ekKc6levRa-BBdtfLeHIP93eO&si=SG5dl_et8sQqwPcs
私もmodの基本をこちらの動画で学習させていただきました。(数学が苦手だしmodを初めて知ったので途中からついていけなくなりましたが、かなりRSAに対する疑問が晴れました。modの威力も。)
まとめ
この記事では、マイナンバーカードの仕組みを入り口に、RSA の動作原理まで丁寧に解説しました。
最後にポイントを整理します。
■ マイナンバーカードの本質は「秘密鍵を安全に守る箱」
- 秘密鍵は IC チップ内から絶対に出ない
- 外部に出るのは「署名結果」だけ
- PC やスマホがウイルス感染していても秘密鍵は盗まれる可能性は低い
■ 病院の窓口では「チャレンジレスポンス」で本人確認
- サーバーが乱数(チャレンジ)を送る
- カードが秘密鍵で署名して返す
- 公開鍵で検証して一致すれば「本人のカード」と証明される
■ 利用者証明用電子証明書には基本4情報が入っていない
- プライバシー保護のため
- 発行番号を使って J-LIS に照会し、署名用電子証明書と紐付けて個人を特定
- 病院には基本4情報は渡らない(資格情報だけが返る)
■ RSA の安全性は「素因数分解の困難さ」に依存
- 公開鍵(N, e)が分かっても秘密鍵 d は求められない
- N を素因数分解できないため
- 2048bit の N は現実的に分解不可能
■ おわりに
マイナンバーカードは「怖い」「危険」というイメージを持たれがちですが、 実際には 非常に堅牢な暗号技術の上に成り立っている ことが分かります。
この記事が、マイナンバーカードや RSA の理解に役立てば幸いです。
時期マイナンバーカードで採用予定のECDSAについては、こちら↓
この記事を書いたイチゲを応援する(質問でもokです)
Vプリカでのお支払いがおすすめです。